Appearance
70 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
1
2
3
4
5
2
3
4
5
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
1
2
3
4
5
6
2
3
4
5
6
提示:
1 <= n <= 45
1
分析题目
这道题目是一个斐波那契数列的问题,可以使用递归的方式解决;
function climbStairs(n: number): number {
if (n === 1) return 1;
if (n === 2) return 2;
return climbStairs(n - 1) + climbStairs(n - 2);
};
1
2
3
4
5
2
3
4
5
结果分析
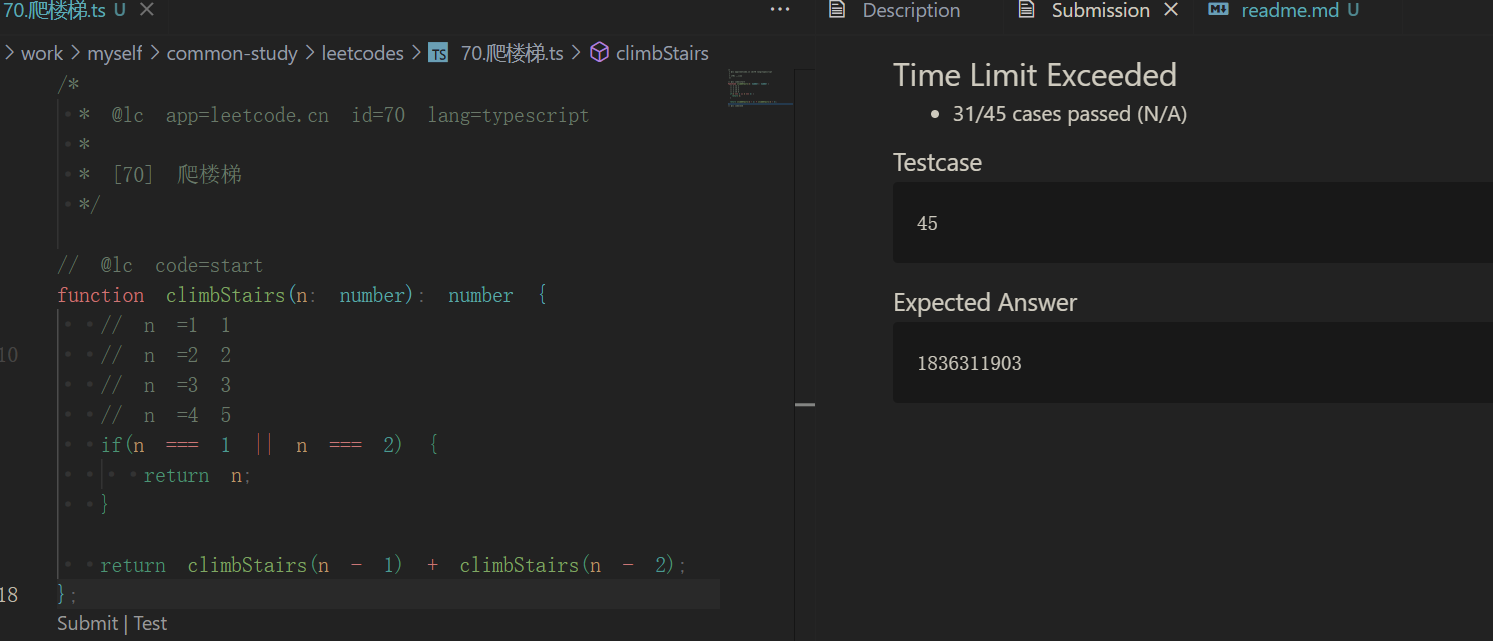
这样做肯定是没有问题的,但是如果数量很大,那么就容易超时
优化
使用动态规划的方式,将每次计算的结果保存起来,避免重复计算
function climbStairs(n: number): number {
// n =1 1
// n =2 2
// n =3 3
// n =4 5
if(n === 1 || n === 2) {
return n;
}
let arr = [1, 2, 3, 5];
for(let i = 4; i <= n; i ++){
arr[i] = arr[i - 1] + arr[i - 2];
}
return arr[n - 1];
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2
3
4
5
6
7
8
9
10
11
12
13
14
结果分析
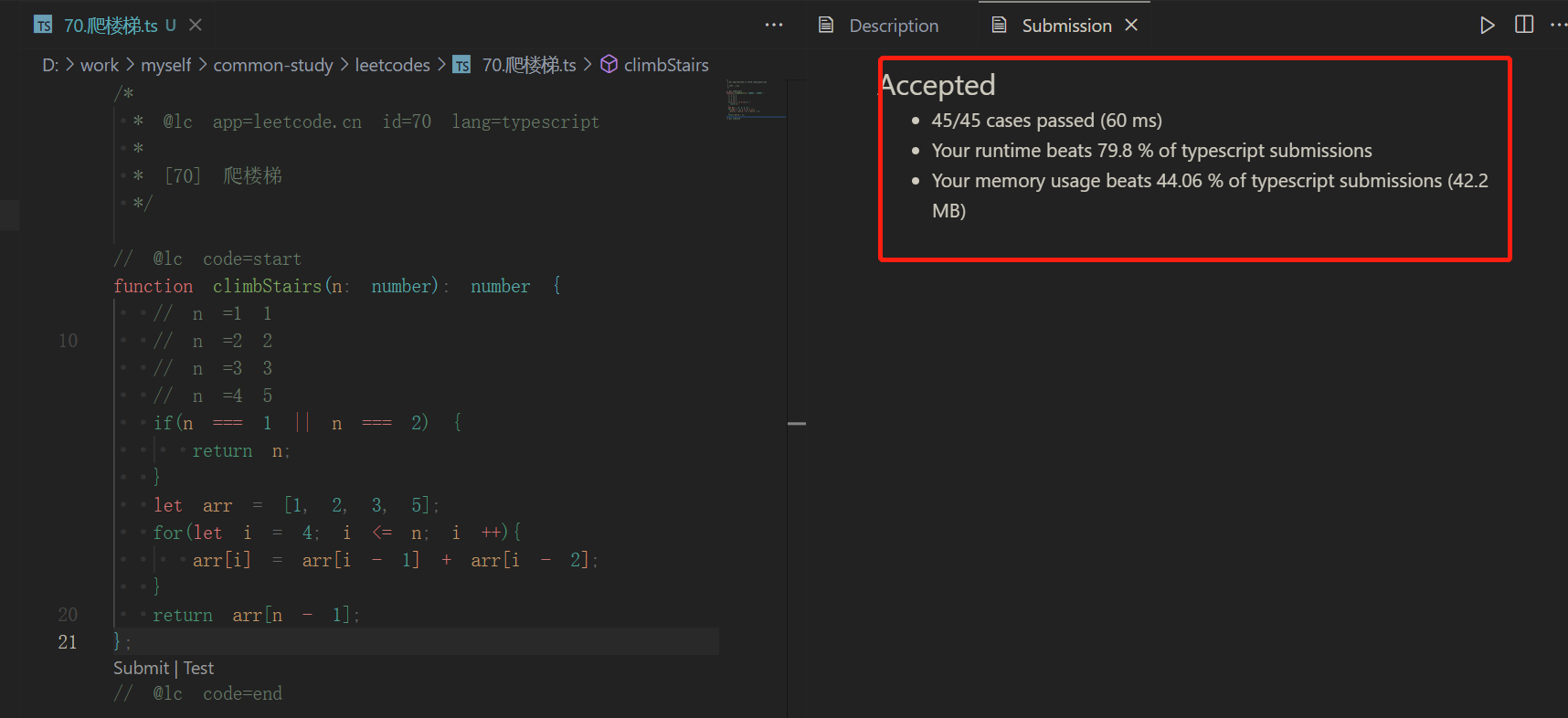
这里使用了一个数组来进行存储数据,但是存储的数据量越大,占用的空间也越大。那么,咋们可以继续优化。
深度优化
在上面使用的是一个数组来装缓存的数据,那么这里可以优化成两个变量
function climbStairs(n: number): number {
// n =1 1
// n =2 2
// n =3 3
// n =4 5
if(n === 1 || n === 2) {
return n;
}
let pre = 1;
let next = 2;
let cur = 3;
for(let i = 2; i < n; i ++){
cur = pre + next;
pre = next;
next = cur;
}
return cur
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
结果
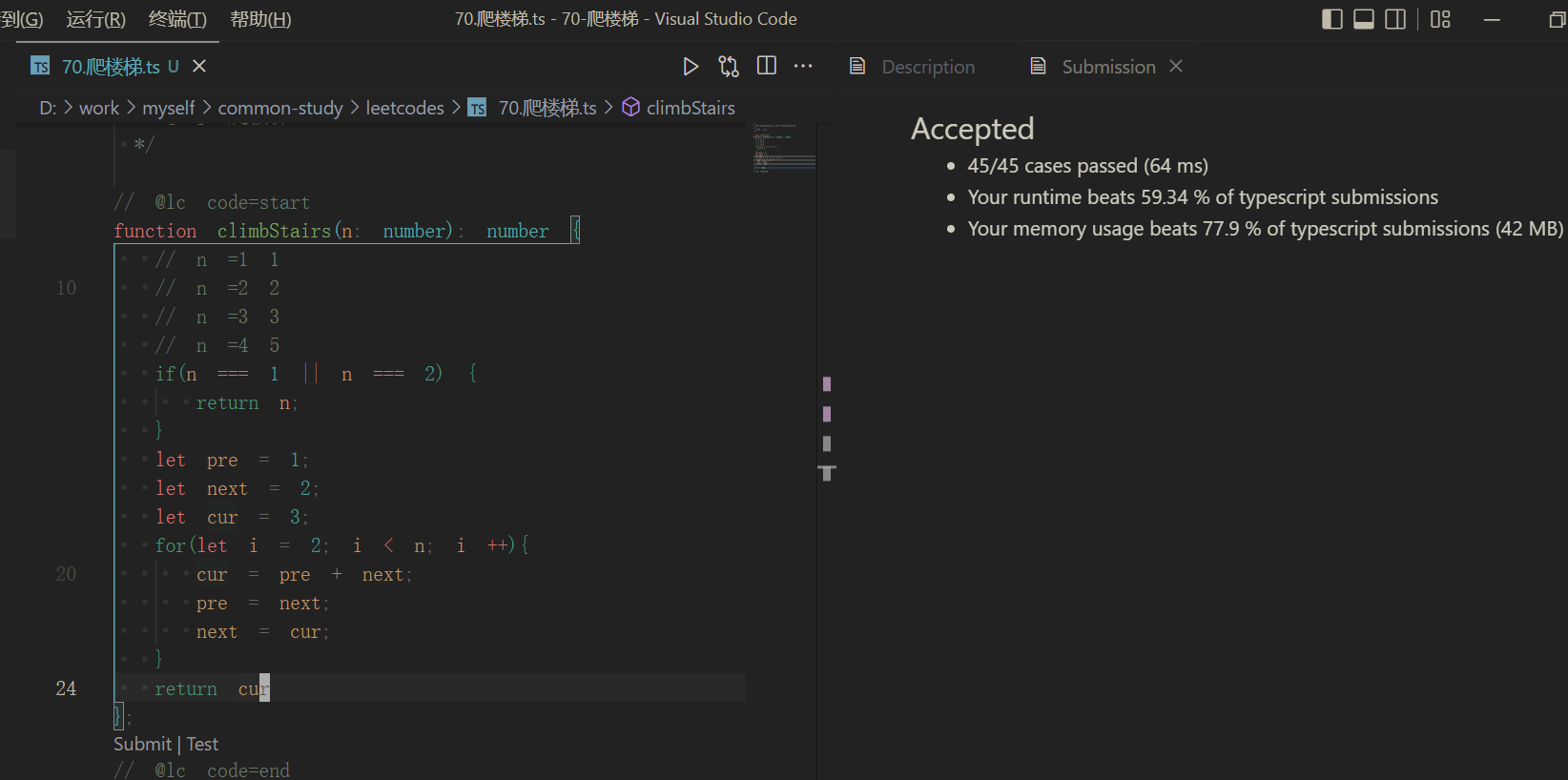
通过者三种方式,可以学习下动态规划的思路。